기본 데이터 유형
Numeric -> 숫자
Character -> 문자
Logical -> 논리값 (TRUE,FALSE)
Factor -> 범주형 변수(Categorical)로 나타낼 수 있는 변수
벡터 생성 -> c(x1,x2,x3)
ex) a <- c(2,4,6,8)
a[2] =4
c$gr[c$gr==0] = 2
c$gr[c$speed <= 17] = 0
d1 = subset(d, sex==1)
library(foreign)
library(lmtest)
library(haven)
library(gmodels)
library(car)
library(survival)
library(dplyr)
library(neuralnet)
library(MASS)
library(Metrics)
library(descr)
library(sas7bdat)
결측치 처리
https://m.blog.naver.com/youji4ever/221449056834
여러 정보
factor() -> 범주형 변수로 취급
데이터 처리 -> tdverse사용해야함
as.Date(d$date)
d=data.frame(date = c("2020-03-26", "2019-05-13", "2020-12-01", "2021-07-18", "2020-09-14"))
d$year=format(as.Date(d$date),format="%Y")
View(d)
exp(0.25891) //obstruct estimate값
-> 1.295517 //의미= 대장암 발병률 1.295배 늘음
데이터 가져오기
getwd() -> 파일 경로 확인
setwd('경로') -> 파일 경로 변경
csv
read.csv(file='smoke.csv', fileEncoding='EUC-KR', header=TRUE)
txt
a=read.table('grades.txt',header=TRUE,sep='\t')
spss
read.spss('',header~)
a <- read_sav("HN22_ALL.sav")
수치형 데이터 표현
boxplot(weight) _> 표로표현
sd(weight) -표준편차
plot() ->산점도
범주형데이터
table() -> 테이블 형식
prop.table() -> 차지하는 비중표현
barplot()
pie()
데이터 표현
lines(cars) -> 점들을 선으로 이어준거 보여줌
lines(lowess(cars)) -> 선을 그어주는데 전체적인 경향성 보여줌
CrossTable(m$vs,m$gear) ->크로스 테이블 생성,상관관계
hist(g$finalgrade) ->히스토그램
mean() -> 산술 평균 구함
median() -> 중앙값
var() -> 분산
sd() -> 표준편차
range() -> 범위(최대 최소)
60세이상 남녀비율
a1=a[,c('age','sex')] -> age, sex만 추출하여 새로운 데이터프레임 만듬
a2=a1[a1$age>=60,]
freq(a2$sex)
결측치 제거
d1 = subset(d, sex==1)
na.omit()
데이터변환
# 숫자로 변환
data$column_name <- as.numeric(data$column_name)
# 범주형으로 변환
data$column_name <- as.factor(data$column_name)
# 날짜로 변환
data$date_column <- as.Date(data$date_column, format = "%Y-%m-%d")
# 열 선택
data <- data[, c("column1", "column2", "column3")]
# 특정 열 제외
data <- data[, !names(data) %in% c("unwanted_column")]
# 조건에 맞는 행 선택
data <- data[data$column_name > 10, ]
데이터 검정
귀무가설 -> ~ 차이가 없을 것이다.
shapiro.test(x) -> 데이터가 정규분포따르는지 확인 (3~5000에서만)
w값이 1에 가까울 수록 정규 분포, p<0.05면 귀무가설 기각(정규분포 따르지 않음)(효과가 있다)
아노바 검정 -> 두 개 이상의 그룹 간 평균 차이를 비교
독립 변수(범주형 변수)가 종속 변수(연속형 변수)에 미치는 영향을 분석할 때 사용
aov(weight~group, data=p) -> 여러 그룹이 weight에 영향 미치는지 분석,그룹간 평균 차이
cor.test -> 두 변수간 상관관계 분석
cor.test(x, y, method = "pearson") -> 피어슨 상관관계 ,정규성 따라야함,선형관계 측정
spearman -> 비선형관계 측정
cor.test(cars$dist,cars$speed) -> cor 값이 양수면 양의 상관관계, dist가 커지면 speed도 커짐
chisq.test ->카이제곱 검정(두 범주형 변수간 독립성 검정)
ex)
chisq.test(mtcars$vs, mtcars$gear)
- : 두 변수는 독립적이지 않다(유의미한 관계가 있음).
- p>0.05p > 0.05: 두 변수는 독립적이다(관계가 없음).
var.test -> 두 그룹의 분산이 동일한지(등분산성)를 검정하기 위해 사용하는 함수
ex)
group1 <- c(10, 12, 9, 11, 10)
group2 <- c(20, 18, 25, 22, 24)
var.test(group1, group2)
- 이므로, 귀무가설(H₀)을 기각.
- 두 그룹의 분산이 동일하지 않다고 결론.
ex)
var.test(A_steps~sex, data = e)
t.test -> 두 그룹 간의 평균 차이가 통계적으로 유의미한지
# 평균이 5와 다른지 검정 t.test(data, mu = 5)
ex)
t.test(A_steps~sex, data = e, var.equal = F)
sex(성별) 그룹에 따라 A_steps(걸음 수)의 평균이 통계적으로 유의미한 차이가 있는지 검정
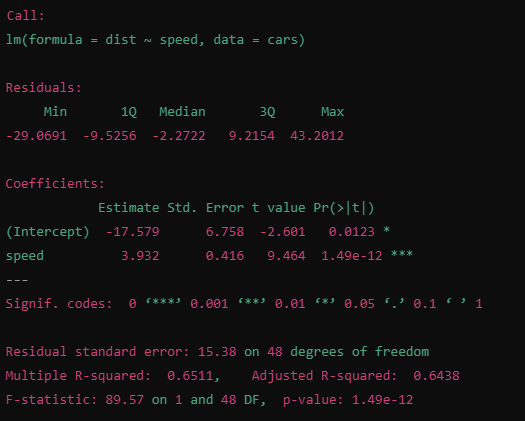
lm(dist ~ speed, data = cars) -> 선형회귀모델, speed를 사용하여 dist예측(단순 선형 회귀 모델)
기울기 봐서 속도가 1증가할때 dist가 얼마나 증가하는지 확인
ex)speed1당 dist 3.932증가
pr 값= p값 유의한지
다중회귀분석 ->여러 독립 변수(설명 변수)가 종속 변수(반응 변수)에 미치는 영향을 분석
ex) lm(mpg ~ hp + wt + cyl, data = mtcars)

- hp:
- 계수: -0.0318. 마력이 1 단위 증가하면 연비(mpg)가 0.0318 감소.
- p-value = 0.00145 < 0.05, 통계적으로 유의미.
- wt:
- 계수: -3.191. 차량 무게가 1 단위 증가하면 연비가 3.191 감소.
- p-value = 0.00021 < 0.05, 통계적으로 유의미.
- cyl:
- 계수: -1.508. 실린더 수가 1 단위 증가하면 연비가 1.508 감소.
- p-value = 0.00104 < 0.05, 통계적으로 유의미.
Multiple R-squared: R2=0.8431R^2 = 0.8431
- 독립 변수들이 종속 변수(mpg) 변동의 약 84.31%를 설명.
p-value ->>
data$g=relevel(data$group, ref=3) ->새로운 변수 지정, 회귀 분석 등에서 범주형 변수를 독립 변수로 사용할 때, 기준 레벨에 따라 결과 해석이 달라지므로 특정 레벨을 기준으로 설정.
ex) lm(value ~ group, data = data)
group의 기본 기준 레벨 (1):
- 다른 레벨(2, 3)은 기준 레벨(1)과의 차이를 비교.
- group의 기준 레벨을 3으로 변경:
- 다른 레벨(1, 2)은 새 기준 레벨(3)과의 차이를 비교.
step() -> 회귀 모델에서 최적 변수 선택을 자동으로 수행( step(lm~~~)), AIC적은게 좋은 모델
VIF -> 다중회귀분석에서 다중공산성(독립 변수간 상관관계)확인 5보다크면 다중공산성이 큼
ex)
model <- lm(mpg ~ disp + hp + wt, data = mtcars)
vif(model) ->
disp hp wt
4.240927 4.085649 2.192234
다중공산성 해결 -> 변수 제거, 변수변환
irtest -> 우도비 검정, 두 개의 선형 모델 또는 일반화 선형 모델(GLM) 간의 적합도를 비교
ex)
m1 <- lm(finalgrade ~ per1grade + per2grade, data = grades) # 완전 모델
m2 <- lm(finalgrade ~ per2grade, data = grades) # 단순 모델
result <- lrtest(m1, m2)
DF -> 자유도
LogLik ->더 클수록 적합도 좋음
- p-value > 0.05 → 단순 모델 채택.
- p-value ≤ 0.05 → 완전 모델(m1)이 더 적합.

glm(finalgrade~per2grade,data=grades)
종속 변수가 이항형, 포아송형 등 다양한 데이터 유형일 때 사용. +카테고리컬
aggregate(weight~group, data=p, mean) -> 데이터를 그룹별로 묶고 weight 평균냄
->
group weight
1 ctrl 5.032
2 trt1 4.661
3 trt2 5.526
# 데이터 준비
data(mtcars)
# 로지스틱 회귀 모델
m <- glm(am ~ wt + hp, data = mtcars, family = binomial)
# 오즈비와 신뢰구간 계산
round(exp(cbind(coef(m), confint(m))), 3) -> 로지스틱 회귀 모델에서 회귀 계수와 신뢰구간의 지수를 계산하고, 결과를 소수점 3자리로 반올림하는 코드
->
Estimate 2.5 % 97.5 %
(Intercept) 0.005 0.000 0.098
wt 0.120 0.015 0.895
hp 1.035 1.001 1.081
- Estimate:
- 회귀 계수를 지수화한 값(오즈비).
- 예: wt의 오즈비는 0.120로, 차량 무게(wt)가 1 단위 증가하면 자동 변속기(am = 1)일 오즈가 약 0.12배로 감소.
- 2.5 %와 97.5 %:
- 회귀 계수의 지수화된 신뢰구간(95%).
- 예: hp의 신뢰구간은 [1.001, 1.081]로, 마력(hp)이 1 단위 증가할 때 오즈비는 이 범위 안에 있을 확률이 95%입니다.
오즈비가:
- 1보다 큼: 해당 독립 변수가 증가하면 종속 변수가 발생할 가능성이 증가.
- 1보다 작음: 해당 독립 변수가 증가하면 종속 변수가 발생할 가능성이 감소.
- 1과 같음: 해당 독립 변수가 종속 변수에 영향을 미치지 않음.
MERGE
e = merge(c1, c3, key = pid) -> pid기준으로 머지,2개씩 해야함
비모수검정 : 데이터가 정규분포하지 않는다 가정, 정규성이나 등분산성 등의 가정을 만족하지 않아도 사용 가능, 표본 적어도 사용 가능
주요 비모수 검정 방법
1. 중앙값 비교
- 단일 표본: Wilcoxon 부호 순위 검정.
- 두 그룹: Mann-Whitney U 검정(Wilcoxon Rank-Sum Test).
- 세 그룹 이상: Kruskal-Wallis 검정.
2. 분포 비교
- Kolmogorov-Smirnov 검정(KS Test).
3. 상관관계 검정
- 스피어만 상관계수(Spearman’s rho).
- 켄달의 타우(Kendall’s tau).
4. 독립성 검정
- 카이제곱 검정(Chi-Square Test).
- 피셔의 정확 검정(Fisher’s Exact Test).